Authors:
(1) Albert Gu, Machine Learning Department, Carnegie Mellon University and with equal contribution;
(2) Tri Dao, Department of Computer Science, Princeton University and with equal contribution.
Table of Links
3 Selective State Space Models and 3.1 Motivation: Selection as a Means of Compression
3.2 Improving SSMs with Selection
3.3 Efficient Implementation of Selective SSMs
3.4 A Simplified SSM Architecture
3.5 Properties of Selection Mechanisms
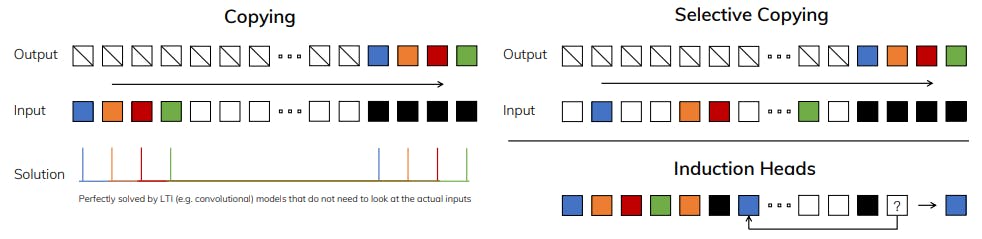
4 Empirical Evaluation and 4.1 Synthetic Tasks
4.4 Audio Modeling and Generation
4.5 Speed and Memory Benchmarks
A Discussion: Selection Mechanism
D Hardware-aware Algorithm For Selective SSMs
E Experimental Details and Additional Results
3.2 Improving SSMs with Selection
One method of incorporating a selection mechanism into models is by letting their parameters that affect interactions along the sequence (e.g. the recurrent dynamics of an RNN or the convolution kernel of a CNN) be input-dependent.


This paper is available on arxiv under CC BY 4.0 DEED license.